Au risque de recevoir les foudres maternelles pour un nième article mathématique, je ne résiste pas au plaisir de partager une méthode pour obtenir une racine carrée d'un nombre, à partir d'une construction géométrique.
Cette construction, connue depuis l'antiquité permet, à partir d'un cercle, de retrouver la racine carrée de n'importe quel nombre, de manière extrêmement simple.
Si l'on prend un segment de droite, que l'on nommera AB (par convention), d'une longueur x. On prolonge AB pour obtenir un segment AC d'une longueur x + 1, puis on trace le cercle ayant pour diamètre AC. On trace ensuite la perpendiculaire en B, qui coupe le cercle en D.
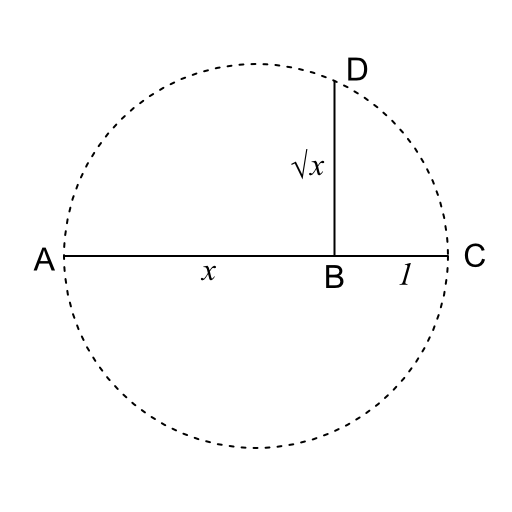
La longueur BD est alors égale à √x
Tous ceux qui ont fait des mathématiques ont, un jour où l'autre, utilisé un x dans une équation, qu'elle soit cartésienne, polynomiale ou diophantienne. Mais pourquoi utilise-t-on la lettre x pour désigner une inconnue?
Cela remonte à Al-Khwarizmi, un mathématicien perse (783 - 850), à qui l'on doit notamment le mot algorithme (cher aux informaticiens) et algèbre, issu du titre d'un de ses livres (ar : al-jabr, la reconstruction). Lorsqu'il avait besoin de désigner une inconnue, Al-Khwarizmi utilisait le mot arabe shay, la chose. Ses ouvrages vinrent en Europe, en passant par l'Espagne où l'inconnue fut traduite en xay.
Puis Descartes, au XVIIè siècle, simplifia cette notation en ne gardant que l'initiale du xay espagnole, d'où le x.
Une anecdote, qui me paraissait moins sérieuse, voudrait que Descartes utilisait la lettre z, dernière de l'alphabet, pour désigner une inconnue. Mais son imprimeur n'avait pas assez de z, mais beaucoup de x.
Source : Wikipedia et ma petite amie pour l'anecdote (je savais bien que j'avais lu cette histoire il n'y a pas longtemps...)
Pour exprimer le nombre d'or ( Φ = (√5 + 1 ) / 2 = 1.61803398...
O nombre d'élégance ! Toi, toi, grandiose, étonnant
Pour se détendre un peu, quelques moyens mnémotechniques inutiles, donc indispensables.
Pour retenir le nombre Pi, il suffit de compter le nombre de lettre de chaque mot du poème suivant :
Que j'aime à faire apprendre ce nombre utile aux sages !
Glorieux Archimède, artiste, ingénieur,
Toi de qui Syracuse aime encore la gloire,
Soit ton nom conservé par de savants grimoires !
Jadis, mystérieux, un problème bloquait
Tout l'admirable procédé, l'œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
0 quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l'espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s'y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l'orbe calculée approchera ;
Définira limite ; enfin, l'arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle.
Königsberg (allemand pour Kaliningrad) est une ville au nord ouest de la Russie, et est à l'origine d'un problème mathématique en théorie des graphes. Königsberg est construite autour de 2 iles, reliées entre elles et au continent par sept ponts. Il est alors impossible, en partant d'un point, de parcourir les septs ponts et revenir à son point d'origine, en ne traversant chaque pont qu'une seule fois.
La résolution de ce problème a été trouvée par Euler, mais vous pouvez toujours aller vous promener a Kaliningrad et chercher tous les chemins possibles.
Source : un épisode de Numb3rs.
